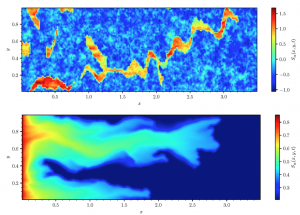
This project corresponds to the theoretical part of the big international collaboration between UFJF, TU Delft and PUC-Rio. The main objective of the project is to improve the understanding of foam displacement in porous media in view of the Enhanced Oil Recovery (EOR) conditions of pre-salt reservoirs. The secondary objective is to develop analytic methods and numerical tools that can be used to test and validate commercial simulators. The project has a strongly multidisciplinary appeal focusing on physical modeling, mathematical analysis and numerical simulations of gas flow (CO2) and surfactant solutions on carbonates leading to foam formation.
(A) The method of in-situ combustion is a thermal technique with great potential for use in the exploration of the offshore oil, as in the case of the pre-salt reservoirs. The modeling of combustion in porous media involves Fluid Dynamics and Chemical Kinetics. The models describing in-situ combustion are composed by reaction-convection-diffusion equations, present different scales (stiff problems) and are difficult to solve both mathematically and computationally.
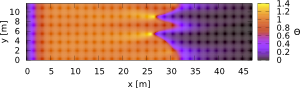
(B) Electromagnetic heating is an non conventional thermal technique based on the transformation of electric energy into thermal energy through the interaction between the electromagnetic field and the particles of the medium.
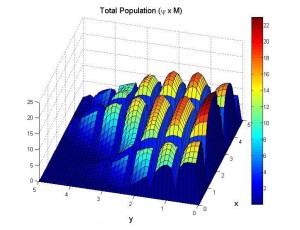
The global incidences of dengue and, more recently, zica virus have increased the interest in studying and understanding the mosquito population dynamics. This project deals with nonlinear mathematical models describing the life cycle of the A. aegypti mosquito using partial differential equations. The methodology involves analytical and numerical techniques from Dynamical Systems, PDEs and Numerical Analysis.
Parabolic-type problems, involving a variational complementarity formulation, arise in mathematical models of several applications in Engineering, Economy, Biology and different branches of Physics. These kinds of problems present several analytical and numerical difficulties related, for example, to time evolution and a moving boundary. We develop numerical methods that employs a global convergent nonlinear complementarity (or mixed complementarity) algorithms for solving a discretized problem at each time step. Space discretization is implemented using the finite difference implicit scheme and the finite element method.